交差エントロピー誤差は多値分類の損失関数としてが用いられ「正解と予測値の交わり具合(差)を定量的に表したもの」になります。
「交差」や「エントロピー」の意味についてはこちらの記事でご紹介をしています。
計算グラフ
早速ですが、交差エントロピー誤差の計算グラフについて確認してみます。
.png)
なぜ計算グラフで理解するのか?
計算グラフで理解するメリットは2つあります。
・難しい計算式を分解し部品化することで「処理の流れ」を簡単に理解することができる
・図で理解するので、忘れにくい。
計算グラフの解説
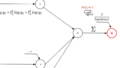
これを踏まえて先ほどの計算グラフを見てみましょう。
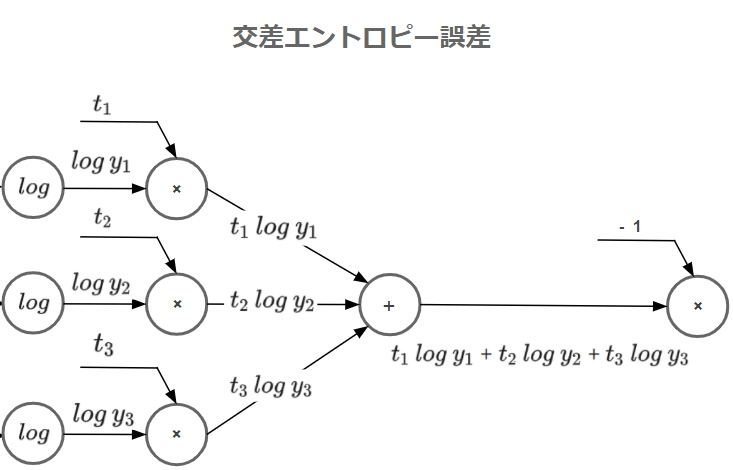
上流からソフトマックス関数の出力値$y$が伝達され、$log$による計算がされます。次に$×$に伝達されますが、ここで新たな入力値として$t$が渡され掛け算がなされます。途中で入ってきた$t$は正解ラベルです。
他の系統でも同じように処理がされたのち、$+$で総和をとります。
最後に$-1$をかけることで交差エントロピー誤差は終了です。
ソフトマックス関数と組み合わせた計算グラフ
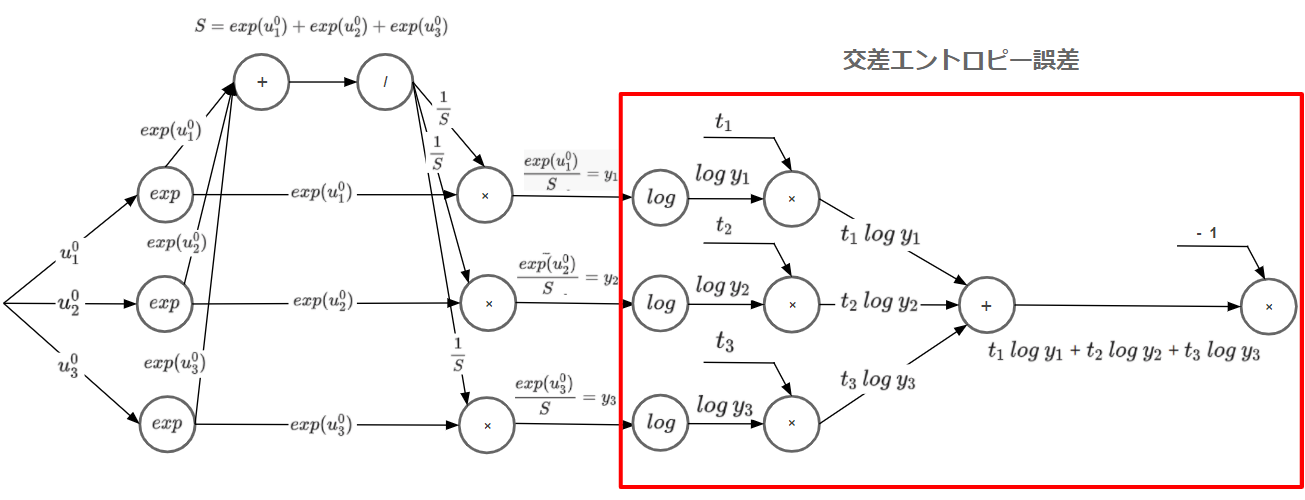
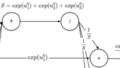
右が交差エントロピー誤差を計算グラフで表したものです。(左はソフトマックス関数)
ソフトマックス関数から出力した値を交差エントロピーの損失関数に流し込み、最終的に1つの誤差として算出されていることがわかります。
計算グラフの効果は誤差逆伝播法で一番の効果を発揮しますが、順伝播でもこのようにソフトマックスとの処理を可視化することで頭の整理ができます。
ここからは具体的な処理を交えながらソフトマックス関数の理解を進めていきます。
簡単なイメージ
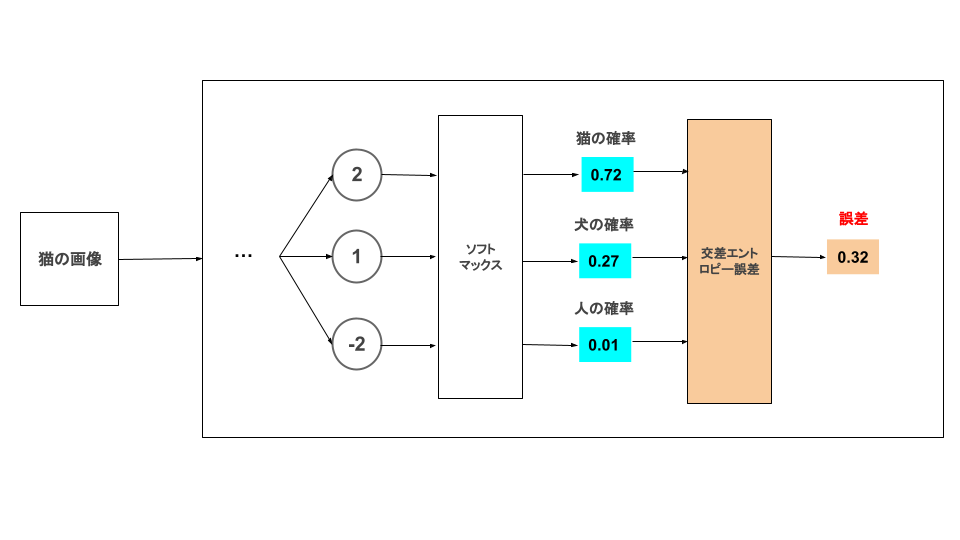
こちらの記事でソフトマックス関数で確率変換した値を交差エントロピーで誤差を算出するイメージ図です。
単純に分類を予測するだけなら損失関数は必要ありません。モデルの精度を上げるため(学習させるため)に損失関数で誤差を算出しています。
交差エントロピーのパターンは3種類
交差エントロピーには取り扱うインプットの形状によって大きく3パターンに分かれます。
■教師データの形状
・One-Hot(今回の記事)
・Not One-Hot
■入力データの形状
・ミニバッチ版
インプットによって処理の違いがある、ということを理解しながら調べないと誤解釈してしまう可能性があるので気を付けてください。
One-Hotでの交差エントロピー誤差
教師データのOne-Hotとはどういうものなのかを見ていきます。
One-Hotとは「正解のインデックスの値が1、それ以外のインデックスの値は0」というデータです。
実際に具体的なデータを使ってみていきます。
## 教師データ
t = np.array([1,0,0])
print(t)
## [1 0 0] → [猫,犬,人]
## ソフトマックス関数で確率変換した予測値
print(y)
## [0.72139918 0.26538793 0.01321289] → 以前の記事で利用した値教師データのOne-Hotは [ 1 , 0 , 0 ] のように正解データが1、それ以外の値が0の配列になっているデータです。ソフトマックス関数で出力した確率の位置がそれぞれに対応しています。
それでは、交差エントロピー誤差で処理をしていきます。
細かいステップの説明の前に最終系で処理をし、その後ステップごとに説明します。
delta = 1e-7
## 交差エントロピー誤差
cross_entropy_error = -np.sum(t * np.log(y + delta))
print(cross_entropy_error)
## [0.326562502647972]交差エントロピー誤差は-np.sum(t * np.log(y + delta))で計算をします。
式でみてもイメージがつかないので図示化します。
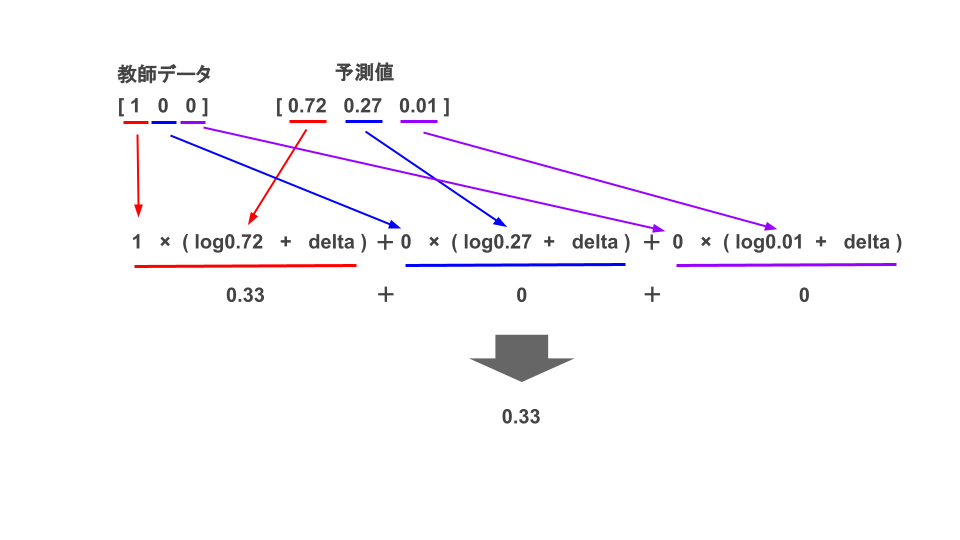
このように教師データと予測値の対応するデータ同士を計算し、最後に総和を取って-1をかけます。
結果、交差エントロピーで処理した結果、正解との誤差は約0.33となりました。
ちなみに計算過程で-1を掛ける理由は、ソフトマックス関数で確率変換され1未満となった各予測値をネイピア数を底にもつlogで計算するとマイナスの値をとるため、-1をかけて正の数にしています。
log_e = np.log(0.6)
print(log_e)
## -0.5108256237659907 ← マイナスの値になる
今回、予測と正解が一致していたため誤差が小さくなっていますが、モデルの予測結果と正解がズレていた場合、どのような大きさの誤差がでるのかみてみましょう。
正解は人だったと仮定して処理をしてみます。
y = np.array([softmax_a,softmax_b,softmax_c])
t = np.array([0,0,1]) ## 正解を人にするため一番右に1をセット
print(y)
## [0.72139918 0.26538793 0.01321289]
print(t)
## [0 0 1]delta = 1e-7
## 交差エントロピー誤差
cross_entropy_error = -np.sum(t * np.log(y + delta))
print(cross_entropy_error)
## 4.326555072927414モデルによると人である確率は1%と予測していますが、正解は人であったので誤差としては約4.3となり、さきほどの結果より13倍も大きい誤差になっています。
つまり、予測値と正解値が違う場合には誤差が大きくなることがわかりました。
① deltaを定義
交差エントロピー誤差の冒頭にdelta = 1e-7を設定します。
1e-7は0.0000001と非常に微小な値を表していますが、なぜ1e-7を足し合わせる必要があるのかをみていきます。
One-Hotは「教師データと予測値の対応するデータ同士を計算する」と説明しました。
その教師データには1と0が存在しますが、0のみで計算するとこのような結果になってしまいます。
log_inf = np.log(0)
print(log_inf)
## -inf” – inf ” という結果になりました。これは負の無限大を意味しており、以降の計算において何を演算しても無限になってしまうという不都合が起こってしまいます。そこで結果に影響を及ぼさないくらい微小な値を足し合わせることで” – inf ” を回避しようという考えです。
delta = 1e-7 ## 0.0000001
log_inf = np.log(0 + delta)
print(log_inf)
## -16.11809565095832微小な値を加えることで” – inf ” を回避できましたね。
②予測値と正解値の乖離具合を計算
つぎにモデルの予測値が正解値に対してどれだけ乖離しているかを計算します。
その計算がt * np.log(y + delta)に該当します。
これは何なんだ一体、と思わず言ってしまいそうな式ですが、ちゃんと格式ある数式になります。
統計力学で分子のバラバラ具合を定量的に表すものとしてボルツマンの関係式があります。
$S=KlogW$
( 概念的な説明はこちらで記載していますので興味がある方は一度目を通してみてください )
この公式を交差エントロピーでそのまま利用しているため、エントロピーという名前がついています。
実際に計算してみます。
print(y) ## [0.72139918 0.26538793 0.01321289]
print(t) ## [1 0 0]
entropy = t * np.log(y + delta)
print(entropy)
## [-0.3265625 -0. -0. ]予測値(y)と正解値(t)の各要素が計算されました。
③誤差の合計を計算
最後に②で算出した各要素の総和をとりマイナス1をかけた結果を誤差とします。
entropy_sum = np,sum(entropy) * -1
print(entropy_sum)
## 0.326562502647972以上が、One-Hotによる交差エントロピー誤差の処理になります。
次回はミニバッチ版の交差エントロピー誤差について説明していきます。
コメント