
小学校とかでプログラミング教育が必修化されたけど、実際にプログラミングを学校で学ぶのかな?

よくわかってないけど、プログラミング的思考を養うことがポイントみたいよ

プログラミング的思考?
論理的思考と何が違うんだろう?

知らないわよ。ググりなさいよ。

で、ですよね・・・。
プログラミング的思考と論理的思考の違い
プロぐミング的思考と論理的思考には多くの共通点があり、中心的な意味は同じです。
いづれも「物事を体系的に整理し、矛盾や飛躍のない筋道を立てる思考法」であることを主としています。
プログラミング的思考はそれに加え、より効率的な思考を加味したものであるという点が違いとしてあります。
文字だけではイメージがしづらいと思いますので、具体的な事例を交えて説明をしていきます。
最短経路は何通り?
さて、問題です。A地点からB地点までの最短経路は何通りあるでしょう?
前提条件としては以下2点。
1.隣接するマス目を辿ること。
2.斜め方向の移動は禁止とする。
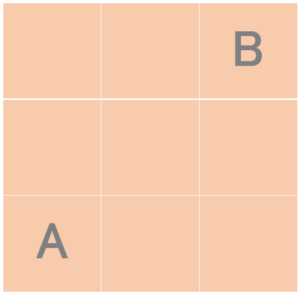
論理的思考
“最短経路”が最大の焦点であるため、最短経路を辿るためには、
・1つの経路探索では同じマス目は通らないほうがよい。
・B地点から遠ざかるような進み方 ( 左方向や下方向 ) はしないほうがよい。
なぜなら、いづれもゴールから遠ざかることになるから。ですね。
このように前提条件の理解・探索条件を思考し「物事に矛盾や飛躍のないルールや方法を定義すること」を論理的思考と言います。
今回は説明のためシンプルな問題を選んでいるため、上記の2つ条件は当たり前すぎて逆にしっくりこないかもしれませんが、最短経路を辿るための条件としては論理的な条件であると言えます。
さて、この問題の答えですが「A地点からB地点までの最短経路は6通り」となります。
思考方法はすごく原始的で、線でなぞってみました。1分もあれば解けますね。
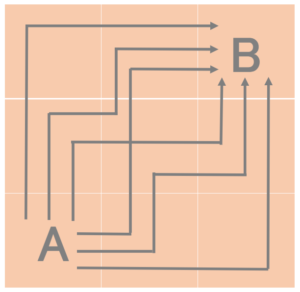
ただ、3 × 3マスの単純な問題だから解けましたが、マス目が増えた場合はどうでしょう?
では、5 × 5マスだったらどうでしょうか?
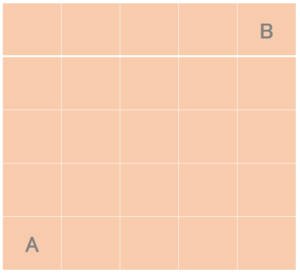
答えは70通りです。
70通りとなると3 × 3マスのときのように線を引きながら解を導くのは難しそうですね。。(頑張ればなんとかできるかな?)
では、10 × 10マスだったらどうでしょうか?
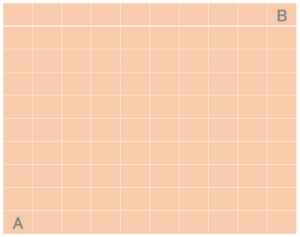
答えは、48,620通りです。
絶対、線なんて引けないですね。。
これからわかるようにしらみつぶしに解を導くやり方ではいづれ限界がきます。
ここまでで分かることは「論理的思考により定義されたものと効率を求めることは別物である」ということです。
かみ砕いて説明すると、今回の問題では”最短経路”を導くために「1つの経路探索では同じマス目は通らないほうがよい」「B地点から遠ざかるような進み方 ( 左方向や下方向 ) はしないほうがよい」という2つの論理的な定義をしましたが、解を導くための手段については言及していません。つまり、論理的に定義されたものに対してどのように実現すれば効率がよいのか?は問うてないということです。
論理的思考に加え「もっと効率的に解を導く方法はないものだろうか?」という思考を加えたものがプログラミング的思考と言います。
プログラミング的思考
プログラミング的思考とは「論理的思考に加え、物事を実現するためにもっとも効率的な手段を考えること」です。
引き続き、先ほどの問題を利用して具体例で説明していきます。
この方法は「各マス目までの最短経路を書き込んでいく」方式です。
・まず1列目、1行目の各マス目は1通りしかないので「1」と書き込みます。
・次にAから右1上1のマス目にいくための最短経路数をそのマス目に書き込みます。(「2」を書き込み )
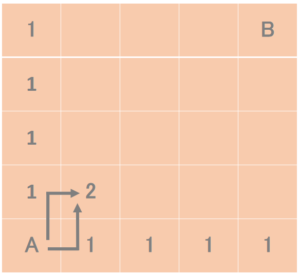
・同じようにAから右2上1、右3上1・・とそれぞれマス目にいくための最短経路数を書き込みます。
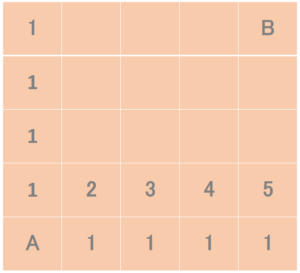
ここで、ある法則があることに気づきましたでしょうか?
「最短経路を求めたいマス目と隣接する左と下の数字を足し込めば最短経路数になる」( △ + △ = 〇になる )という法則です。
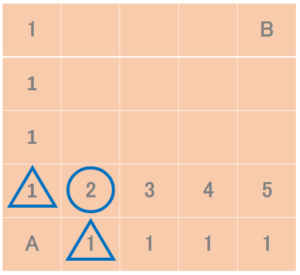
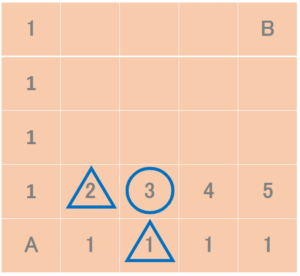
この法則に従って続けていくと、以下のようになります。

図からもわかるようにA地点からB地点までの最短経路数は70通りとなります。
この書き込み方式であればものの数分で解くことができました。
明らかに線でなぞるより早くて正確ですね。
このように同じ解を導くために効率的な方法を考えることがプログラミング的思考になります。
プログラミングとは?
プログラミングとは「コンピューターに実行してほしい処理をコンピューターが理解できる言葉で記載すること」です。
コンピューターに苦手意識がある人は「うっ・・」となるかもしれませんが、日本語や英語と同じだと思ってもらっても大丈夫です。英語しか読めない・話せない人に仕事をお願いしようと思った場合、英語で伝えるしか手段がないのと同じような感覚です。
さっきの最短経路を導く問題で考えてみましょう。
コンピューターに「AからBへいく最短経路を教えて」と書いても何も教えてはくれません。
どのような手順でどのように計算するのか?を具体的に記載してあげる必要があります。
プログラミング的思考で利用した書き込み方式「最短経路を求めたいマス目と隣接する左と下の数字を足し込めば最短経路数になる」をプログラミングするとこのような感じになります。
def counting(a, b):
A = [[-1 for j in range(b + 1)] for i in range(a+1)]
for i in range(a+1):
A[i][0] = 0
for j in range(b+1):
A[0][j] = 0
A[1][1] = 1
for i in range(1, a+1):
for j in range(1, b+1):
if A[i][j] == -1:
A[i][j] = A[i-1][j] + A[i][j-1]
print("{}行目{}列にいく経路は{}通り".format(i, j, A[i][j]))
return A[a][b]
counting(5,5)何がなんだかわからなくて大丈夫です。
少し説明しておくと、counting(5,5)のカッコ書き部分はマス目の数を表していて、ここの数字を変えることでマス目に応じた最短経路を導くことができます。
このようにプログラム化することで非常に効率的な手段を手にすることができます。
プログラムを書くこと自体は慣れれば難しくありません。慣れさえすれば、人が言葉を話すのと同じようにサラサラと書くことができます。
重要なのは思考
プログラム化することで非常に効率的な手段を手にすることができますが、どのような手順でどのように計算するのか?を考えるのは人であり、それを考えることが自体に相当な訓練が必要となります。
小学校、中学校、高校でプログラミングが必修化されましたが、文部科学省が発行している資料内ではこのように記述されています。
プログラミングに取り組むことを通じて、児童がおのずとプログラミング言語を覚えたり、プログラミングの技能を習得したりするといったことは考えられるが、それ自体をねらいとしているのではない。
「プログラミング技能を習得ことがねらいではない」とはっきり記述されています。
あくまでもプログラミング的に思考する能力を高めること重要である。ということです。
以上、今回の記事が参考になれば幸いです^^




コメント