ディープラーニングをやり始めの時はとりあえずググって、誰かのブログに書いてあることをコピペで実行しながら「おー、できたー」という感じがだいたいの始まりかと思います。
その後、自分で撮った画像とかを学習させながら新たなモデルを作ってみたりしますが、そのうちこんな疑問がでてきます。
「そもそも、学習ってなんだ？どういう仕組みなんだ？」
超、基礎。でも、基礎ってホント大事。
いや、基礎が大事ってわかってながらも、基礎からやっても頭に入らないんですよ、実際のところ。
自ら何かを始めるときって、興味がある範囲からやって「できたー」的な喜びを感じてからようやく、そもそもこれってどういう意味なんだっけ？ってなるなーって最近思いました。
で、いざ調べ始めるとドツボにハマりました。
目の当たりにするのは微分や統計、損失関数がどうだの、活性化関数がどうだのと小難しいことばかりで、「自分には無理だ・・・」と途中でやめようかとも思いました。
でもやっぱ気になるので、本見たり、ググったり、Youtubeみたりといろいろ苦労し、ようやく理解することができました。
そのおかげで、今では構造を理解しながら一からモデルを作れるようにまでになりました。
決して、賢いわけでも、要領がいいほうでもないです。むしろ逆です。
そんな私ですから、一からモデルを作れるようになるまでだいぶ遠回りをしましたが、世の中には自分と同じように悩んでいる人も多いと思うのと、改めて自分の中で整理する意味合いも含めて自分がつまづいた箇所をくわしく記録していきたいと思います。
ディープラーニング
ディープラーニングとは
改めて復習です。
” 人間が特徴を与えなくても、データから自動で特徴を抽出し、自動で学習し賢くなる仕組み “ です。
ディープラーニングの定義とは
入力層、隠れ層、出力層の合計が4層以上あるものがディープラーニングとして定義されています。
図で表すとこんな感じ。
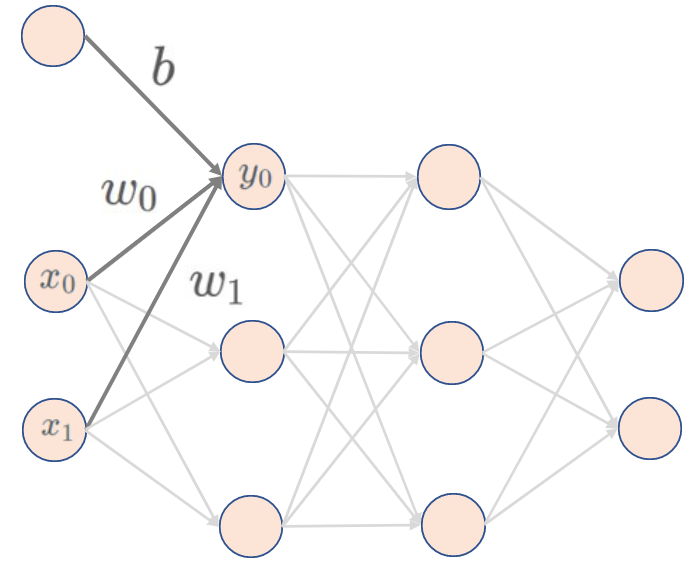
入力層の入力データ($x_0$や$x_1$)に重み($w_0$や$w_1$)とバイアス($b$)という変数が加えられ、次のニューロン($y_0$)へ伝えられていきます。式にすると以下の通りです。
\[y_0 = w_0x_0 + w_1x_1 + b\]
このようなネットーワーク構造をニューラルネットワークと呼び、与えられた入力データからデータの特徴を自動的にとらえ、いい感じに学習しながら予測モデルを構築していきます。
ディープラーニングにおける「学習」とは
学習とは、最適な重み($w$)とバイアス($b$)を見つけることです。
では、どのようにして最適な重み($w$)とバイアス($b$)を見つけるのでしょうか？
それは、入力データで学習したモデルが出力した予測結果($y$)と正解($t$)との間違い具合を計算し、この間違いを補正しながら最適な解を見つけていきます。
文章にすると数行のことなのですが「じゃあ、具体的に何してるの？」と聞かれると難しくないですか？
今回のゴール
この記事を読み終える頃には、ディープラーニングの ” 学習の仕組み “ を誰かに説明できるようになることをゴールとします。
また、この記事を読むことで学習に必要な以下の3つの式も説明できるようになります。
現時点、式の内容が意味不明でも大丈夫です。
「3つの式が大切なんだな」ということくらいに留めておいてください。
誤差関数(平均二乗和誤差)の式
\begin{align}
E&=\frac{1}{2}Σ(t_i-y_i)^2\\
&=\frac{1}{2}Σ(t_i-(w_ix_i+b))^2
\end{align}
重み($w_i$)を更新する式
\begin{align}
w_i&=w_i-η\frac{∂E}{∂w_i}\\
&=w_i−η(Σ((w_ix_i+b)−t_i)∗x_i)
\end{align}
バイアス($b$)を更新する式
\begin{align}
b&=b-η\frac{∂E}{∂b}\\
&=b−η(Σ(w_ix_i+b)−t_i)
\end{align}
課題設定
これから説明していくモデルは、
$x=3$が与えらたとき$y=7$、$x=9$が与えらたとき$y=13$
を予測するモデルの学習の過程を説明していきます。
連立方程式で解けばいいじゃん、はナシです。
では、やっていきましょう
ますは話の中心となる式を見ておきます。
$y_0 = w_0x_0 + b$ (1.1)
今回、入力データ($x$)に対する正解値($y$)をモデルの学習時に渡すので、重み($w$)とバイアス($b$)が変数となります。(←学生時代は$x$と$y$を変数として問題を解くことが多かったので頭をシフトしましょう)
ディープラーニングは入力データ($x$)と正解値($y$)をモデルに与えるだけで、自動的に重み($x_0$)とバイアス($b$)をいい感じ（←これが今回の解説ポイント）計算してくれる素敵なヤツです。
今回は学習の過程を理解するためなので、最終的に求めたい式（いい感じの式）を定義しておきます。（もちろん、このいい感じの式は最初から分かっているものではなく、学習の過程でいい感じに求められていきます）
$y_0 = x_0 + 4$
最終的に求めたい重み($w_0$)を1、バイアス($b$)を4と定義しています。
この式どっから出てきたの？と思われる方もいるかもしれないので一応言っておきますが、テキトーです。
あくまでもどうやって学習していくのか？というのが今回の趣旨なので、計算しやすい値を選びました。
ここで視覚的に確認してみましょう。
最終的に求めたい、いい感じのグラフを右、学習開始時のグラフを左に書きました。
青丸と赤丸を分離する線形を学習で見つけていきます。
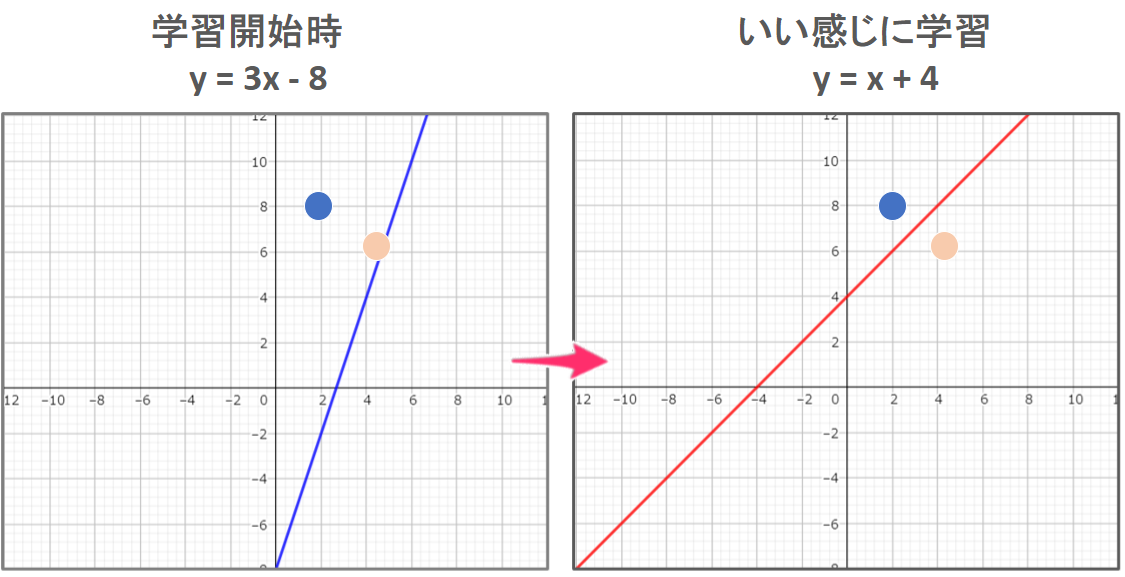
あれ？学習開始時の式はどっから出てきたの？と思われるかもしれません。
学習開始時の重み($w$)、バイアス($b$)ともに適当な値で学習が開始されます。
適当な重みとバイアスで学習を開始し、モデルが出力した予測結果($y$)と正解($t$)との間違い具合を計算し、この間違いを補正しながら最適な解を見つけていくということをやってます。
グラフに話を戻しますが、左のグラフを見ると、青丸と赤丸をうまく分離するような線形にはなっていませんね。
この状態から入力データ($x$)を大量に読み込みんで、正解値($t$)と答え合わせしながら、重み($w$)をこんな感じ？バイアス($b$)はこんな感じ？という具合にごにょごにょしながら徐々にいい感じのモデル(右のグラフ)を構築していきます。
改めていい感じの式と、学習開始時の式を見ておきましょう。
いい感じの式 ：$y_0 = x_0 + 4$ (1.2)
学習開始時の式：$y_0 = 3x_0 – 8$ (1.3)
もう一度言いますが、いい感じの式は初めからはわかっていない（求めるべき答え）ので、一旦忘れます。
さて、ここからはモデルを学習していく流れに沿ってみていきます。
学習開始時の式に入力データと正解データを放り込む
さて、(1.3)で定義した式に入力データ($x$)と正解値($t$)を放り込んでいきますが、その前にそもそも(1.3)は適当に決めた式でしたね。
なぜ、適当に決めたもので学習を進めるのでしょうか？
それは、始める段階では正解が何かわからないから、です。
正解がわからないから適当に式を作って、そこから学習をして精度を高めていくということをしていきます。
どうやって精度を高めるのかというと、冒頭に書いた「入力データ($x$)で学習したモデルが出力した予測結果($y$)と正解($t$)との間違い具合を計算し、この間違いを補正しながら最適な解を見つける」ことでモデル精度を高めていきます。
実際、具体的な値を使ってみていきます。入力データと正解データ以下の通りです。
① 入力データ：$x_0=3$、正解値：$t_0=7$
② 入力データ：$x_1=9$、正解値：$t_1=13$
では、(1.3)の式に①②を放り込んでいきましょう。
①入力データ：$x_0 = 3$ 正解値：$t_0 = 7$
先ほど定義した(1.3)の式に入力データ($x_0$)の3をいれて計算してみます。
なお、ここでの正解値($t_0$)は7です。
$y_0 = 3x_0 – 8\ = 3 × 3 – 8 = 1$ (1.4)
計算の結果、予測値($y_0$)は1と算出されました。
正解値($t_0$)が7なので、予測値($y_0$)と一致しませんね。
つまり、(1.3)の式では、モデルとしての精度が悪いということが言えます。
■入力データ：$x_1 = 9$ 正解値：$t_1 = 13$
次も同様に先ほど定義した(1.3)の式にインプットデータ($x_1$)の3をいれて計算してみます。
なお、ここでの正解値($t_1$)は13です。
$y_1 = 3x_1 – 8\ = 3 × 9 – 8 = 19$ (1.5)
計算の結果、予測値($y_1$)は19と算出されました。
正解値($t_1$)が13なので、予測値($y_1$)と一致しませんね。
これも先ほど同様、(1.3)の式では、モデルとしての精度が悪いということが言えます。
2つのインプットデータをつかってモデルの精度を確認しましたが、予測値と正解値が乖離しているので、モデルの精度を上げなければいけません。
どれくらい精度が悪いのか？
先ほど計算した結果では、モデルの予測値($y$)と正解値($t$)が一致しませんでした。
この精度って、何をもって良くて、何をもって悪いと言えるでしょうか？
少し考えてみてください。
・・・
・・・
はい、答えは「予測値($y$)の値と正解値($t$)の値が近ければ近いほど良いモデル」ということが言えます。
つまり、予測値($y$)が正解値($t$)に近づくようにするためには、重み($w$)とバイアス($b$)をいい感じに調整すればよいことがわかります。
お互いが近づくためにはお互いの距離を埋めていけばいいですね。つまり、予測値($y$)と正解値($t$)の差をまずは知る必要があります。
それでは、(1.4)(1.5)で計算した予測値と正解値の差をみていきます。
①入力データ：$x_0 = 3$ 予測値：$y_0 = 1$ 正解値：$t_0 = 7$
$E_0$(差)：$t_0 – y_0 = 7 – 1 = 6$ (1.6)
②入力データ：$x_1 = 9$ 予測値：$y_1 = 19$ 正解ラベル：$t_1 = 13$
$E_1$(差)：$t_1 – y_1 = 13 – 19 = -6$ (1.7)
それぞれの差が出たのでどれくらい正解値($t$)と離れているのか計算してみましょう。
\[E_0 + E_1 = 6 + (-6) = 0\]
あれ、ゼロになってしまいましたね。
これでは差が分からないので、マイナスが発生しても差がわかるように差を計算するときに２乗しておきます。
$E_0$(差)：$( t_0 – y_0 )^2 = ( 7 – 1 )^2 = 36$ (1.8)
$E_1$(差)：$( t_1 – y_1 )^2 = (13 – 19)^2 = 36$ (1.9)
$E = E_0 + E_1 = 36 +36 = 72$ (2.0)
これで差が$E = 72$であることがわかりましたね。
この誤差を求める流れは最初に記述した誤差を求める式「誤差関数(平均二乗和誤差)」の意味になります。
もう一度みておきます。
誤差関数(平均二乗和誤差)の式
\begin{align}
E&=\frac{1}{2}Σ(t_i-y_i)^2\\
&=\frac{1}{2}Σ(t_i-(w_ix_i+b))^2
\end{align}
おー、確かに正解値($t$)から予測値($y$)を引き算して二乗してますね。
あれ？一番前の$\frac{1}{2}$って何ですか？？
これはコンピューター上の計算を軽くするために$\frac{1}{2}$しています。
それ以上の理由はないので「軽くするために$\frac{1}{2}$してるんだな」で大丈夫です。
一応、(2.0)を$\frac{1}{2}$しておきます。
$E = \frac{1}{2} * ( E_0 + E_1 ) = 36$
ここまででモデル精度の悪さ加減を確認することができました。
まとめ
今回はモデルの精度の悪さをどうやって評価するのかを説明してきました。
次回は「いい感じの重み($w$)を見つけにいこう」と「いい感じのバイアス($b$)を見つけにいこう」です。
コメント