前回の記事では【計算グラフで理解する】交差エントロピー誤差 -One-Hot版-を解説しました。
今回はミニバッチ版を解説していきます。(本解説を先にすることで次回解説予定の「Not One-Hot版」の理解がしやすくなると思います)
ミニバッチとは
「一定のデータの塊を処理する単位」をバッチと言います。
例えば今、手元に1,000枚の画像データがあるとします。この1,000枚の画像データからランダムに100枚を学習用データとして切り出し、ニューラルネットワークに流し込み、学習を行うとします。このとき、1,000枚から100枚の画像データを1つの塊として抽出し、学習させることをミニバッチ学習と呼びます。
「ミニバッチっていうくらいだから、バッチ学習もあるの?」と疑問に思われた方のために補足します。
データを流し込む単位は3種類あります。
・ミニバッチ
・バッチ
・オンライン
今回の本題ではないので詳細は割愛しますが、以下の特徴があります。
| 学習単位 | 学習安定性 |
外れ値の影響 |
学習速度 | メモリ負荷 (負荷の少なさ) |
|
| ミニバッチ | 一定の塊 | 〇 | 〇 | 〇 | 〇 |
| バッチ | すべて | ◎ | ◎ | △ | △ |
| オンライン | 1件ずつ | △ | △ | ◎ | ◎ |
それぞれにメリット・デメリットがありますが、モデル構築においてはミニバッチが利用されることが多いです。
機会があれば解説のページを作りたいと思います。
ミニバッチ版の説明前提
ミニバッチ版の交差エントロピー誤差の具体的な説明に入る前に前提となる条件を設定しておきましょう。
■条件
・最終出力層の分類は3つ
・インプットの画像データは1,000枚で、1バッチサイズを100枚とする。
計算グラフ
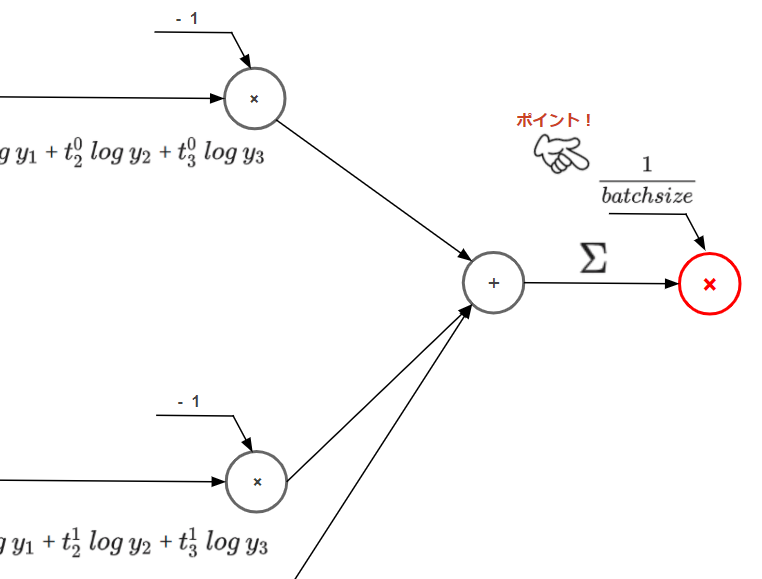
着目すべきポイントは最後にバッチサイズで割る箇所です。
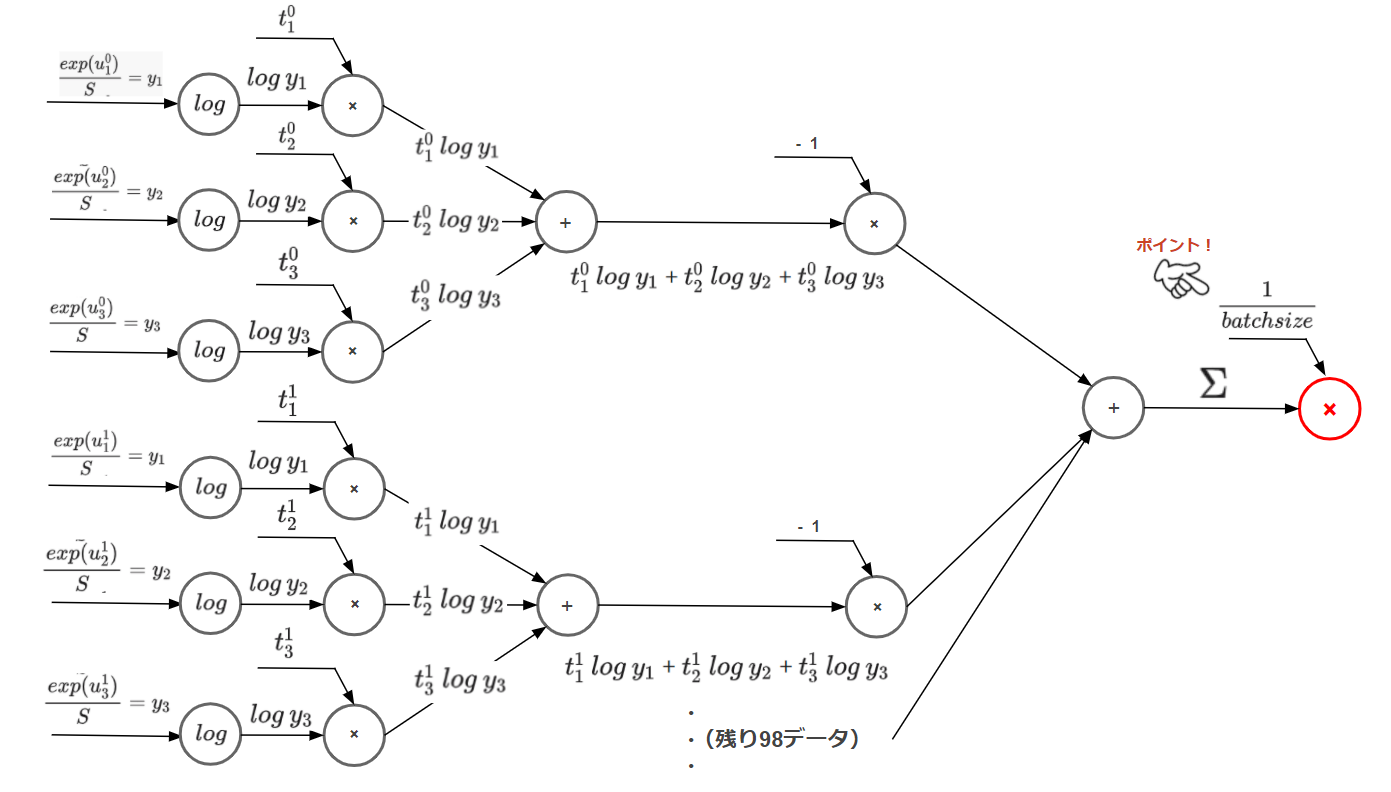
前回の記事で1データだけ処理するときには含まれていなかったステップです。
ミニバッチで処理するときは100枚で1つの単位として処理するため、1つ1つのデータの損失を足し合わせ、バッチサイズ(今回は100)で割ることで1データあたりの平均損失を計算する必要があるためです。
私もまだ勉強中の身ではありますが、学習したての頃はバッチサイズで割るケースと割らないケースの明確な切り分けが分かっておらず理解がフワフワしていたので、同じような人の疑問解消になればと思います。
特に今後解説予定である、誤差逆伝播でだいぶ混乱をしていた時期がありました^^;
実装
つぎに実装の解説になります。
基本的には前回記事のコード内容に対してバッチサイズで割るステップを追加するだけになります。
最初に結論となる実装内容を示したあとに各ステップを解説していきます。
■交差エントロピー誤差(ミニバッチ版)
def cross_entropy_error_batch(y,t):
delta = 1e-7
return -np.sum ( t * np.log( y + delta )) / batch_size
■ミニバッチ処理
batch_size = 100
idx = np.random.choice(y.shape[0],batch_size)
print(idx)
## [365 263 180 893 691 221 335 637 594 479 903 589 756 951 466 4 976 642
## 233 819 895 647 845 112 929 516 296 775 475 815 628 671 99 917 162 633
## 81 58 469 493 976 745 727 447 845 613 885 740 361 145 903 354 172 719
## 114 372 806 859 415 734 114 103 579 686 351 938 142 579 20 446 300 563
## 905 282 168 844 535 742 155 157 652 771 909 627 269 27 323 833 186 227
## 229 927 422 217 67 261 425 498 5 283]
y_train = y[idx]
print(y_train.shape)
## (100, 3)
t_train = t[idx]
print(t_train.shape)
## (100, 3)
E = cross_entropy_error_batch(y_train,t_train) ## 交差エントロピー誤差で損失を計算
print(E)
## 1.3621181234900572結果として、100データ分(1バッチ分)の損失は1.3621181234900572となりました。
交差エントロピー誤差(ミニバッチ版)の定義式
def cross_entropy_error_batch(y,t):
delta = 1e-7 ## -infを回避
return -np.sum ( t * np.log( y + delta )) / batch_size ## バッチサイズで割る前回記事で解説した定義式に対してbatch_sizeで割っているだけのシンプルな構造となります。
基本式については前回解説してますので、ここでは割愛をします。
バッチサイズ設定とインデックス取得
つぎはバッチサイズと母集団データからのデータ抽出です。
事前の条件設定として「1,000枚の母集団から100枚を1バッチのサイズとして処理する」としていましたのでそれに従い実装します。
batch_size = 100 ## 1バッチサイズを100とする
idx = np.random.choice(y.shape[0],batch_size) ## 10,000個の予測値からバッチサイズ分のデータのインデックスをランダムに取得
print(idx) ## 取得したインデックス
## [365 263 180 893 691 221 335 637 594 479 903 589 756 951 466 4 976 642
## 233 819 895 647 845 112 929 516 296 775 475 815 628 671 99 917 162 633
## 81 58 469 493 976 745 727 447 845 613 885 740 361 145 903 354 172 719
## 114 372 806 859 415 734 114 103 579 686 351 938 142 579 20 446 300 563
## 905 282 168 844 535 742 155 157 652 771 909 627 269 27 323 833 186 227
## 229 927 422 217 67 261 425 498 5 283]batch_sizeは100として設定します。
次にidxとしている部分ですが、1,000件の予測値から1バッチサイズ分をランダムに抽出します。抽出するのはデータそのものではなくて、インデックス情報を抽出します。
インデックス情報から予測データを取得
つぎに1,000件の予測データから100件分のデータを取得しますが、抽出対象データの特定はさきほど取得したインデックス情報に紐つくデータを取得します。
y_train = y[idx] ## 取得したインデックスと合致する予測データを取得
print(y_train.shape)
## (100, 3)インデックス情報から正解データを取得
同じく、1,000件の正解データから100件分のデータを取得します。抽出方法はさきほどと同様です。
t_train = t[idx] ## 取得したインデックスと合致する正解データを取得
print(t_train.shape)
## (100, 3)1バッチサイズ分の損失を計算
最後に取得したデータの損失を計算します。
E = cross_entropy_error_batch(y_train,t_train) ## 交差エントロピー誤差で損失を計算
print(E)
## 1.3621181234900572
以上が交差エントロピー誤差(ミニバッチ版)の処理となります。
次回はこれを踏まえて、Not One-Hot版を解説します。
コメント