前々回はOne-Hot版、前回はミニバッチ版を解説してきました。
これらを踏まえて今回はNot One-Hot版を解説していきます。
Not One-Hotとは?
One-Hotは分類する数だけ要素を持っていましたが、Not One-Hotは正解のインデックスのみで構成される正解データです。
文書ではイメージしづらいので少し図示化してみます。
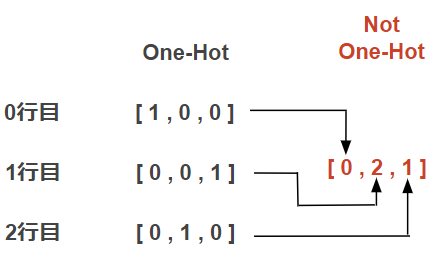
図のように正解要素のみを抜き出したデータで構成されているのがNot One-Hotです。
Not One-HotのメリットはOne-Hotよりデータ量が少ない分、処理が軽量になるという点です。ただでさえ何万件、何十万件とある学習データで計算コストが大きいのに、正解データも比例して大きくなることは避けたいですよね。
どのように損失を計算するのか?
最初に結論となるコードみていきます。その後、各ステップの解説をします。
batch_size = 100 ## 1バッチサイズを100とする
delta = 1e-7
idx = np.random.choice(y.shape[0],batch_size) ## 10,000個の予測値からバッチサイズ分のデータのインデックスをランダムに取得
print(idx) ## 取得したインデックス
## [753 654 782 11 486 854 807 527 249 496 392 627 294 70 630 581 82 313
## 813 524 660 851 549 363 737 218 938 285 204 364 969 318 656 774 5 963
## 820 795 822 497 785 455 392 844 247 108 365 907 638 269 586 142 272 385
## 492 766 498 408 49 860 788 748 998 99 713 566 834 648 593 453 639 732
## 868 747 428 994 52 280 870 146 726 936 710 807 167 956 101 656 139 834
## 938 688 969 39 995 265 743 408 456 155]
y_train = y[idx] ## 取得したインデックスと合致する予測データを取得
print(y_train.shape)
## (100, 3)
t_train = t[idx] ## 取得したインデックスと合致する正解データを取得
print(t_train.shape)
## (100, 3)
### これより上の解説は前回記事を参照してください ###
t = t_train.argmax(axis=1)
E = -np.sum(np.log(y[np.arange(batch_size), t] + delta)) / batch_size
print(E)
## 1.275536533021017One-Hotから正解インデックスを取得
t = t_train.argmax(axis=1)の解説をします。
t_trainはOne-Hot形式のデータで、t_trainの各行で最大値が格納されている列(インデックス)を取得します。
t_trainの各行の最大値を格納した結果は以下の通りです。
print(t)
## [0 1 2 1 0 1 1 1 0 0 2 1 1 0 0 1 2 0 0 1 0 1 0 0 1 2 2 2 1 1 0 2 0 1 2 0 0
## 2 2 1 2 2 2 1 1 2 2 1 2 0 0 2 2 2 2 0 2 2 0 0 2 2 2 0 0 0 1 2 0 0 0 2 2 1
## 2 1 2 0 0 0 0 0 0 1 1 0 1 0 0 1 2 2 0 0 2 2 0 2 0 2]正解ラベルに該当する予測データを取得
y[np.arange(batch_size), t]の解説にうつります。
前述の通り、Not One-Hotの正解データは正解のインデックスのみが格納されているので、次に各行から正解インデックスの位置に該当するデータを取得します。
イメージでみていきましょう。
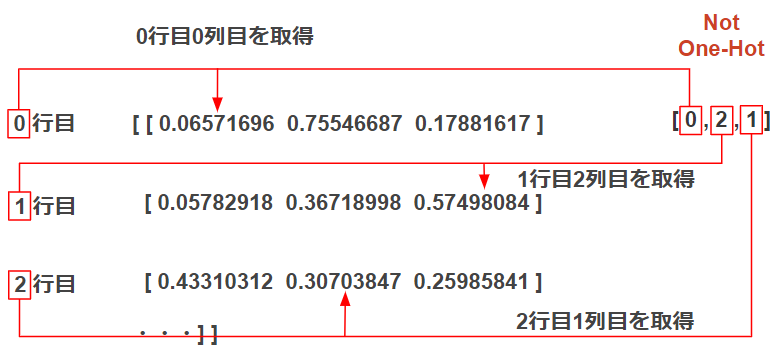
各行ではソフトマックス関数で出力された確率が並んでいます。0行目に対応する正解データのインデックスを見ると0列目が正解データとなっているので「0行目の0列目」の予測値を取得します。
同じように1行目、2行目・・・と繰り返し取得し、各行から正解ラベルに該当する予測値を取得します。
y[np.arange(batch_size), t]を使って補足説明すると0行目はy[0, 0]となり「予測データの0行0列目を取得」します。
対数をとったあと総和をとりバッチサイズで割る
-np.sum(np.log(y[np.arange(batch_size), t] + delta)) / batch_sizeの解説になります。
先程、y[np.arange(batch_size), t]は計算したのであとは式通りに計算するだけです。
前回記事でも解説していますが、最後にbatch_sizeで割るのは1データあたりの平均損失を計算するためです。
今回はNot One-Hotの解説をしました。最初の頃は同じ交差エントロピー誤差でもなんで計算式が違うのだろう??と混乱してました^^;
同じように理解が進まなかった人が、今回の記事で解決に繋がればと思います。
次回はソフトマックス関数と交差エントロピー誤差の誤差逆伝播について解説を予定しています。
コメント