さて、いよいよ誤差逆伝播法がやってきました。
この誤差逆伝播法に何回心をへし折れたことか・・・
今、悩みまっしぐらの方も諦めずに続ければ道は開けます。一緒に頑張りましょう。
誤差逆伝播法とは?
誤差逆伝播法とは「損失関数で計算した誤差を限りなくゼロに近づけるために、重みとバイアスを調整する方法」です。
“誤差”を出力層から入力層に向かって”逆”に”伝播”させることから「誤差逆伝播法」と言います。意識高い系サイトでは「Backpropagation(バックプロパゲーション)」と言ったりもします。
なぜ難しく感じるのか?
誤差逆伝播法を調べるとほとんどのサイトで「連鎖律」や「合成関数の微分」というキーワードが頻出します。
$\dfrac{\partial L}{\partial w}=\dfrac{\partial L}{\partial o}\dfrac{\partial o}{\partial u}\dfrac{\partial u}{\partial w}$
「連鎖律とは」「微分とは」のように誤差逆伝播法を理解するためにはまずは数学を理解しなければいけないというのが一番のハードルになっている気がします。
今回は連鎖律を勉強しなくても理解できる「計算グラフ」を使って解説をしていきます。
この記事で理解できること
・誤差がどのように逆伝播しているかがわかる。
・ソフトマックス関数の逆伝播がわかる。
・交差エントロピー誤差の逆伝播がわかる。
・全結合層での逆伝播がわかる。
前提となる知識は、ソフトマックス関数の順伝播および交差エントロピー誤差の順伝播の仕組みが理解できていることを前提とします。
交差エントロピーの誤差逆伝播
さっそく計算グラフをみていきます。
【計算グラフで理解する】交差エントロピー誤差 -ミニバッチ版-で説明した順伝播の計算グラフに赤字で逆方向に追記したものが誤差逆伝播です。
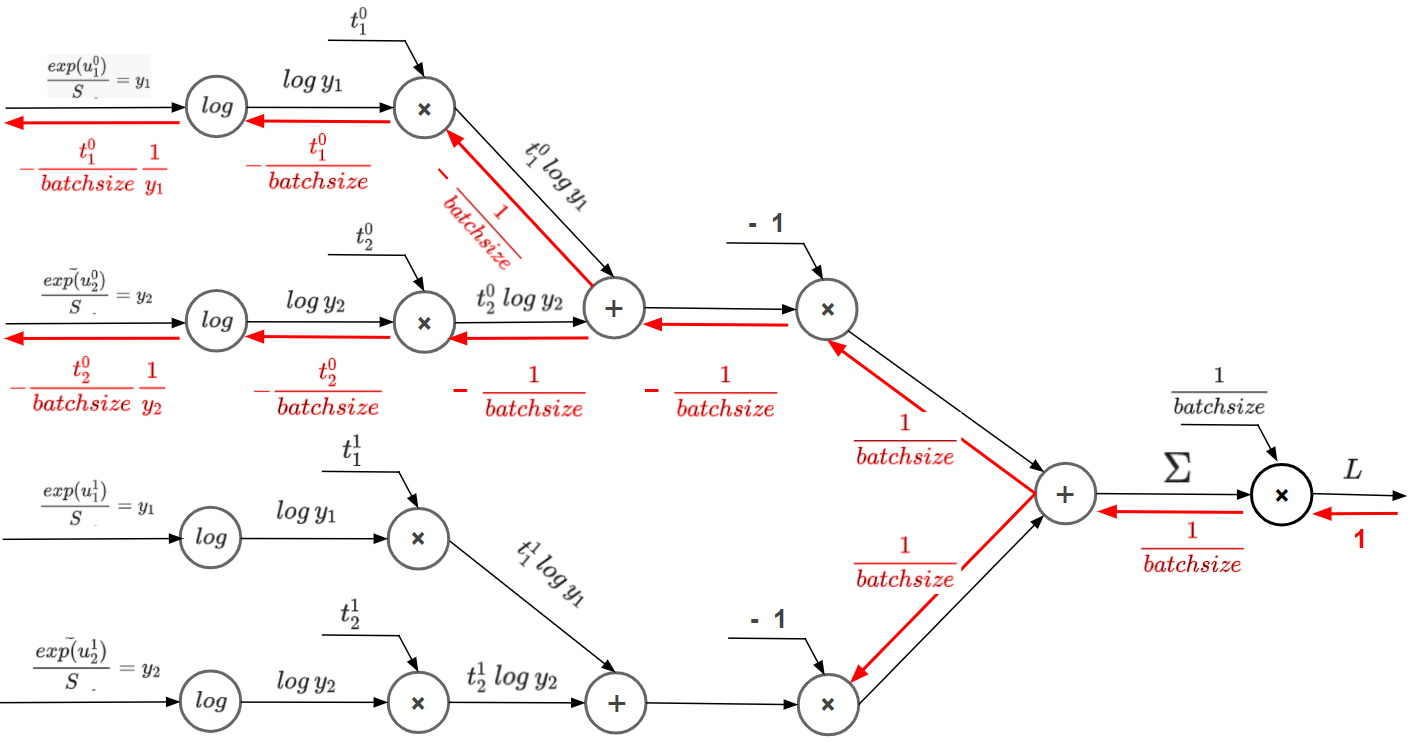
3つのルール
交差エントロピー誤差の誤差逆伝播を理解するのには3つのルールを理解する必要があります。
それは各ノード(丸の部分)に掛かれている演算子の取り扱いです。
| 演算子 | ルール |
| + | 逆伝播してきた値をそのまま次のノードへ受け渡す |
| × |
順伝播時の値を「ひっくり返して」次のノードへ受け渡す |
| $log$ | $log$ $xの場合、\dfrac{1}{x}$とする |
これさえ覚えれば難しい数式を理解しなくても理解することができます。
今回の解説では一番上のルートを解説していきます。(他のルートもやり方は同じなので省略します)
誤差逆伝播のスタートは「1」
まずは一番右の値に注目してください。
一番右では、順伝播で損失を計算した誤差を$L$として表現しており、ここが誤差逆伝播のスタート地点です。
そして逆伝播のスタートを「1」としていますが、適当に「1」と置いたわけではなく、誤差逆伝播のスタートは1で始まります。これは損失を損失で約分しているためです。
$\dfrac{\partial L}{\partial L}$
真剣に理解すればしようとするほど、こういう何気ない数字でも「なんで1なの?説明のためにとりあえず1にしてるの?」と疑問を抱いてしまいますよね^^;
1つ目のニューロン「×」
ここでは「×」のルールに従って、順伝播時の値をひっくり返して次のノードへ受け渡します。
①順伝播の時は $Σ$ と $\dfrac{1}{batchsize}$ が流れてきていますのでこれをひっくり返す。
②次に逆伝播で流れてきた 1 にひっくり返した $\dfrac{1}{batchsize}$ を掛けて次のニューロンへ受け渡す。
結果、次のニューロンには $\dfrac{1}{batchsize}$ が流れていきます。
ひっくり返されたもう一つの値($Σ$)は、次に受け渡すニューロンがないので捨てられます。
2つ目のニューロン「+」
次は「+」のルールに従って、逆伝播してきた値をそのまま次のノードへ受け渡します。
逆伝播してきた値は$\dfrac{1}{batchsize}$ですので、何も手を加えずにそのまま次のニューロンへ受け渡します。
3つ目のニューロン「×」
次は「×」のルールに従って、順伝播時の値をひっくり返して次のノードへ受け渡します。
①順伝播の時は $t^0_1$ $log$ $y_1$ + $t^0_2$ $log$ $y_2$ と -1 が流れてきていますのでこれをひっくり返す。
②次に逆伝播で流れてきた $\dfrac{1}{batchsize}$ にひっくり返した -1 を掛けて次のニューロンへ受け渡す。
結果、次のニューロンには $-\dfrac{1}{batchsize}$ が流れていきます。
ひっくり返されたもう一つの値($t^0_1$ $log$ $y_1$ + $t^0_2$ $log$ $y_2$)は、次に受け渡すニューロンがないので捨てられます。
4つ目のニューロン「+」
次は「+」のルールに従って、逆伝播してきた値をそのまま次のノードへ受け渡します。
逆伝播してきた値は $-\dfrac{1}{batchsize}$ ですので、何も手を加えずにそのまま次のニューロンへ受け渡します。
5つ目のニューロン「×」
次は「×」のルールに従って、順伝播時の値をひっくり返して次のノードへ受け渡します。
①順伝播の時は $t^0_1$ と $log$ $y_1$ が流れてきていますのでこれをひっくり返す。
②次に逆伝播で流れてきた $-\dfrac{1}{batchsize}$ にひっくり返した $t^0_1$ を掛けて次のニューロンへ受け渡す。
結果、次のニューロンには $-\dfrac{t^0_1}{batchsize}$ が流れていきます。
ひっくり返されたもう一つの値($log$ $y_1$)は、次に受け渡すニューロンがないので捨てられます。
6つ目のニューロン「$log$」
最後は「$log$」のルールに従います。
①順伝播の結果をルールに従い、$log$ $y_1=\dfrac{1}{y_1}$ とします。
②次に逆伝播で流れてきた $-\dfrac{t^0_1}{batchsize}$ に①を掛けて次のニューロンへ受け渡す。
結果、次のニューロンには $-\dfrac{t^0_1}{batchsize}$$\dfrac{1}{y_1}$ が流れていきます。
ここまでが交差エントロピー誤差の誤差逆伝播です。
「×」「+」「log」のたった3つのルールを使うだけで、誤差逆伝播を理解することができました。
次回説明するソフトマックス関数も同じで、簡単なルールを覚えるだけで難解な誤差逆伝播を理解することができます。
是非、次回もお楽しみに!
コメント