ディープラーニングを学べばもれなくついてくる交差エントロピー誤差。
必ず出てくるので一度は勉強するのですが後々「交差エントロピーってなんだったっけ?」「平均二乗誤差との使いわけってどうしてたっけ?」みたいな疑問がでてきます。
そんなことをずっと繰り返しその都度調べるのが面倒になってきたので自分の備忘録としてまとめておきます。
そんな交差エントロピーですが、名前からして取っつきにくいヤツですが、中身は非常にシンプルです。
$$ E = -\sum_{k}\ t_k log y_k $$
交差エントロピー誤差の特徴
・3つ以上の分類タスク(多値分類)で利用
・logの底はネイピア数($ e $)
・活性化関数のソフトマックス関数と合わせて利用
・確率的勾配降下法と相性が良い
“エントロピー”ってなに?
原子的排列および運動状態の混沌(こんとん)性・不規則性の程度を表す量。
全っ然、わかりません。。説明聞いて逆に頭が混沌としてマス…(=_=)
エントロピーをわかりやすい表現になおすと、” 状態のバラバラ具合を表すもの ” です 。
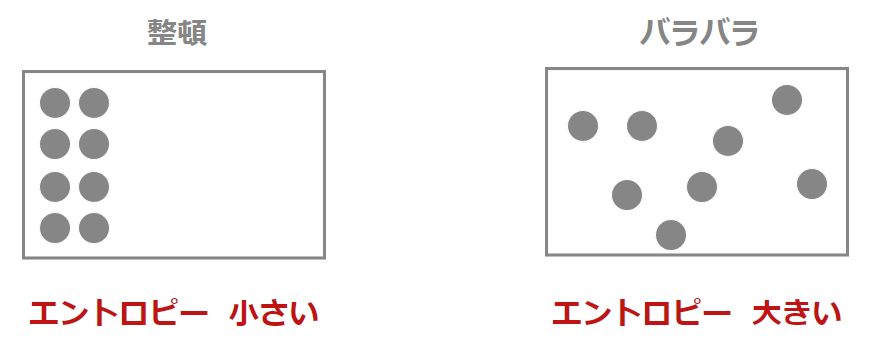
交差エントロピー誤差では正解と予測値のエントロピー、つまり、バラバラ具合を計算しているんですね。
ちなみに交差エントロピー誤差はディープラーニングの世界で初めて定義されたものではなく、物理の世界で定義された公式を用いています。物理学では「物事というのは放っておくと、バラバラになる性質がある」という特徴をこの公式を使って定量化しています。身近にある例でいうと、
・氷は自然に溶けるが、溶けたものが自然に固まることはない。
・拡散した気体は元には戻らない。
といったように日常に起こる変化がエントロピーというもので定義できるということです。
“交差”ってなに?
二つ(以上)の線状のものが、十文字やすじかいに交わること
何が交わるの?って感じですが、ディープラーニングの世界では「2つの確立分布がどれくらい離れているか、つまり、どれくらい交差しているか」を表現するものです。
いや、わからん…
という気持ちはわかりますが、これを正確に理解するのであれば統計学の知識が必要になります。
ここでは交差エントロピーを理解することを優先にしていているので敢えて咀嚼していうと「正解と予測値の2つの交わり具合」を交差と呼ぶことにします。
まとめ
交差エントロピー誤差とは「正解と予測値の交わり具合(差)を定量的に表したもの」になります。
平均二乗誤差も正解と予測値の差を表したものですが、物理学の世界で利用されているエントロピーを採用しているものが交差エントロピー誤差になります。

コメント