前回の続きです。
前回はモデルの精度の悪さ加減を見る方法を説明しました。
この3つの大切な式について記載しましたが、今回は「重みを更新する式」と「バイアスを更新する式」の解説をしていきます。
誤差関数(平均二乗和誤差)の式(←前回)
\begin{align}
E&=\frac{1}{2}Σ(t_i-y_i)^2\\
&=\frac{1}{2}Σ(t_i-(w_ix_i+b))^2
\end{align}
重み($w_i$)を更新する式(←今回)
\begin{align}
w_i&=w_i-η\frac{∂E}{∂w_i}\\
&=w_i−η(Σ((w_ix_i+b)−t_i)∗x_i)
\end{align}
バイアス($b$)を更新する式(←今回)
\begin{align}
b&=b-η\frac{∂E}{∂b}\\
&=b−η(Σ(w_ix_i+b)−t_i)
\end{align}
いい感じの重み($w$)を見つけにいこう
誤差を求めた結果、もっと精度を高める必要がわかりましたので、いい感じの重み($x$)とバイアス($b$)を見つけていきましょう。
そもそも求めたい式を思い出してみましょう。
$y_0 = w_0x_0 + b$ (1.1)
あー、でしたね。入力データ($x$)と正解値($t$)は与えられるので、重み($w$)とバイアス($b$)が変数でしたね。
いい感じのモデルは誤差がゼロに近いことを求められているので、誤差関数(平均二乗和誤差)に(1.1)を代入してみます。
\begin{align}
E_0 &= \frac{1}{2} × (t_0 – y_0)^2 = \frac{1}{2} × ( t_0 – ( w_0x_0 + b ) )^2\\
E_1 &= \frac{1}{2} × (t_1 – y_1)^2 = \frac{1}{2} × ( t_1 – ( w_0x_1 + b ) )^2\\
E &= E_0 + E_1 = \frac{1}{2} × (( t_0 – ( w_0x_0 + b ) )^2 + ( t_1 – ( w_0x_1 + b ) )^2))\\
&= \frac{1}{2} × (( 7 – ( 3w_0 + b ) )^2 + ( 13 – ( 9w_0 + b ) )^2)\\
&=\frac{1}{2} × ((b^2+6w_0b-14b+9w_0^2-42w_0+49 ) + ( b^2+18w_0b-26b+81w_0^2-234w_0+169 ))\\
&= \frac{1}{2} × (2b^2+24w_0b-40b+90w_0^2-276w_0+218)\\
&= b^2+12w_0b-20b+45w_0^2-138w_0+109$ (2.2)
\end{align}
差を求めた理由は、差を計算した(2.2)の式がゼロに近づけたいので、
$$0 = b^2+12w_0b-20b+45w_0^2-138w_0+109 (2.3)$$
になるような$w_0$と$b$を導いていきます。
すぐ忘れるので、念のため書いておきます。
(2.3)は、誤差の合計を求めるために展開したものです。
これがゼロになる、つまり、それが理想のモデルだということです。
これってどんなグラフ?
式長いし、変数が2つもあるし、これってどんな感じのグラフなんでしょう?
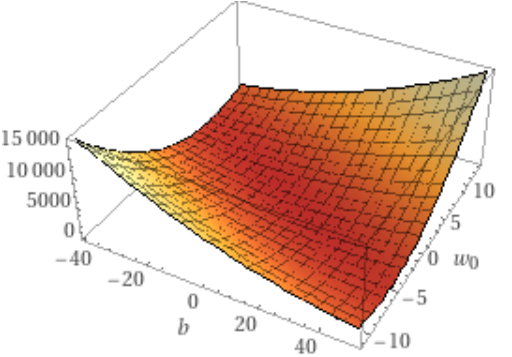
げっ、何これ。この3次元の最適な重み($w$)とバイアス($b$)求めるの大変そうですね。
ということで中学校で習った連立方程式に直していきます。そのときに偏微分を用いて対応していきます。
偏微分とは微分する対象以外は定数と扱って微分することです。
■(2.3)の式を$w_0$で偏微分
\begin{align}
0 &= b^2+12w_0b-20b+45w_0^2-138w_0+109\\
&= 0 + 12b – 0 + 90w_0 – 138 + 0\\
&= 90w_0+12b-138 (2.4)
\end{align}
■(2.3)の式を$b$で偏微分
\begin{align}
0 &= b^2+12w_0b-20b+45w_0^2-138w_0+109\\
&= 2b + 12w_0 -20 + 0 -0 + 0\\
&=12w_0+2b-20 (2.5)
\end{align}
偏微分で求めた(2.4),(2.5)を連立方程式で解いていきます。
$0=90w_0+12b-138$ (2.4)
$0=12w_0+2b-20$ (2.5)
これを解くと、$w_0=1$、$b=4$になります。
おぉ!最初に定義したいい感じの式、$y_0 = x_0 + 4$ (1.2)になりました!
おいおいおいおい、、
めでたしめでたし。じゃねーよ。
(1.3)で適当に決めた重み($w$)とバイアス($b$)でごにょごにょ計算したのはどこいったんだよ?
なんか煙に巻かれた感じがすんだけど?
ですよね。。そこを今から解説していきます!
気合いを入れた瞬間に心が折れる
でもね、解こうとしている(2.3)のグラフって、こんな感じなんです。(2回目)

僕の頭ではこんな3次元グラフで説明できるほど、頭よくないっす。。。
じゃあ、どうすんだよ?
(2.3)の式は変数が2つある且つ2次関数なので、これを1変数2次関数にすれば解けそうです。
$b^2+12w_0b-20b+45w_0^2-138w_0+109$ (←2変数2次関数)
これを1変数2次関数にするにはどちらかの変数を定数を入れればいいですね。
どちらでもいいのですが、今回は学習開始時のバイアス($b$)を-8で固定し、計算してみます。
\begin{align}
0&=(-8)^2+12w_0 * (-8) – 20 * (-8) +45w_0^2-138w_0+109\\
&=64 – 96w_0 + 160 + 45w_0^2 – 138w_0 + 109\\
&=45w_0^2 – 234w_0 + 333 (2.6)\\
\end{align}
ちなみにこんなグラフになります。
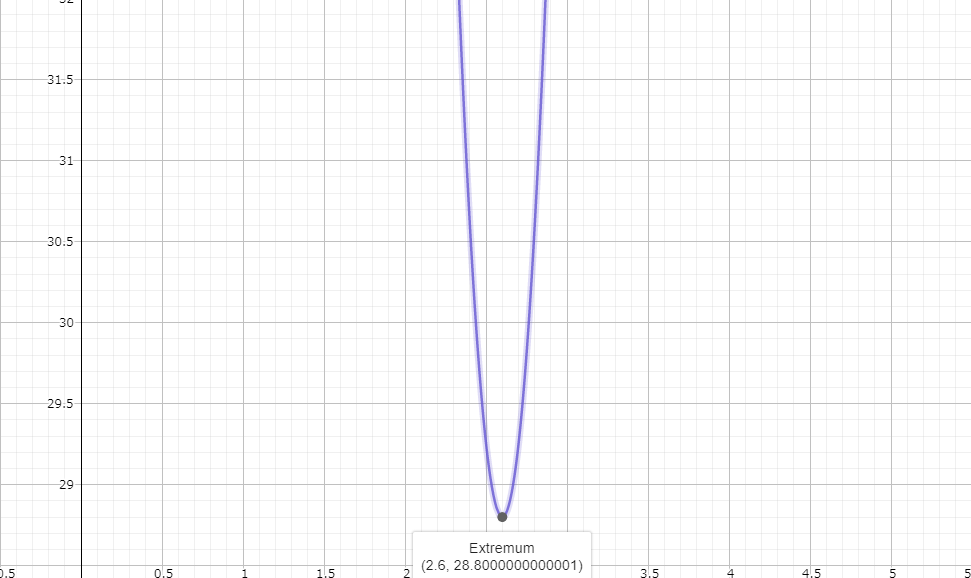
横軸$w=2.6$が最小値となることがグラフから読み取れますが、実際はこんな単純ではないので、どうやって最小値を求めていくのかを説明します。
誤差がゼロ($w=2.6$のところ)、つまり傾きがゼロになるようにすればいいので、今、自分が放物線上のどこにいるか確認して、最小値に近づいていく重み($w$)を求めればいいですね。
傾きを求めるには微分すればいいので、(2.6)を微分しましょう。
\begin{align}
0&=45w_0^2 – 234w_0 + 333\\
&=90w_0-234 (2.7)
\end{align}
微分した(2.7)に学習開始時の重み($w$)の3を入れてみます。
$$90w_0-234 = 90 × 3 -234 = 36$$
重み($w$)が3のときに、傾きが36であるということを意味します。
傾きが正の値をとったので、右肩上がりのグラフであることがわかります。
最小値に近づけるためには、横軸$w$の値を左に持っていけばいいことがわかります。
ということで重み($w$)を徐々に小さくしていってみましょう。
■重み($w$)を2.9にしてみる
$w=2.9のとき、90w_0-234=90 × 2.9-234=27$
傾きが減りましたね。
■重み($w$)を2.8にしてみる
$w=2.8のとき、90w_0-234=90 × 2.8-234=18$
傾きが減りましたね。
■重み($w$)を2.7にしてみる
$w=2.7のとき、90w_0-234=90 × 2.7-234=9$
傾きが減りましたね。
■重み($w$)を2.6にしてみる
$w=2.6のとき、90w_0-234=90 × 2.6-234=0$
傾きがゼロになりました!
■重み($w$)を2.5にしてみる
$w=2.6のとき、90w_0-234=90 × 2.5-234=-9$
あら、傾きがマイナスで出始めましたね。
ということで、(2.7)の重み($w$)が最小値になるのは$2.6$であることがわかりました。
バイアス($b$)を-8にしたときの重み($w$)が求まったので
これを式にしてみましょう。
$$ y= 2.6x -8$$
これに入力データ:$x_0 = 3$、正解値:$t_0 = 7$を入れてみてモデルの精度(誤差)を計算してみましょう。
\begin{align}
E&=2.6x -8\\
&=2.6 × 3 – 8\\
&=7.8 – 8 \\
&=-0.2
\end{align}
$E_0$(差):$( t – y_0 )^2 = 7 – ( -0.2 )^2 = 51.84$
①入力データ:$x_1 = 9$、正解ラベル:$t = 13$
\begin{align}
&E=2.6x -8\\
&=2.6 × 9 – 8\\
&=23.4 – 8 \\
&=15.4
\end{align}
$E_1$(差):$( t – y_1 )^2 = (13 – 15.4)^2 = 5.76$
$E=E_0+E_1=51.84+5.76=57.6$
差が57.6となりましたので、(1.8)(1.9)より誤差が小さくなったので正解に近づいたことになりました。
ただ、まだまだ誤差が大きいので適当にいれたバイアス($b$)-8は不適切そうだ、ということがわかりますね。
次の式を試してみよう
-8では精度が悪かったので、学習開始時のバイアス($b$)に4をいれてみましょう。
\begin{align}
0&=4^2+12w_0 × 4 – 20 × 4 +45w_0^2-138w_0+109\\
&=16 + 48w_0 – 80 + 45w_0^2 – 138w_0 + 109\\
&=45w_0^2 – 90w_0 +45 (2.8)\\
\end{align}
ちなみにこんなグラフになります。
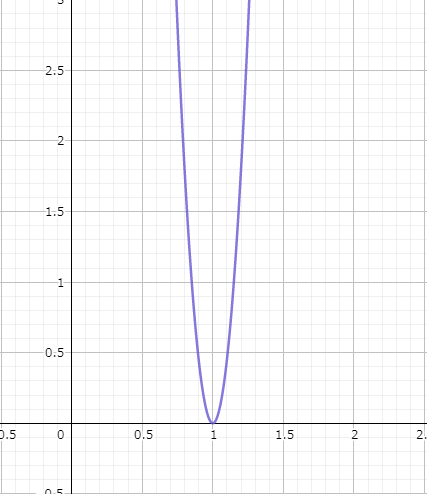
いや、もう、$x=1$じゃん。
ってなりそうですけど、実際はもっと複雑なので簡単には分かりません(2回目)
傾きを求めるには微分すればいいので、(2.8)を微分しましょう。
\begin{align}
0&=45w_0^2 – 90w_0 + 45\\
&=90w_0-90 (2.9)
\end{align}
微分した(2.9)に学習開始時の重み($w$)の3を入れてみます。
$$90w_0-90 = 90 × 3 – 90 = 180$$
重み($w$)が3のときに、傾きが180であるということを意味します。
傾きが正の値をとったので、右肩上がりのグラフであることがわかります。
最小値に近づけるためには、横軸$w$の値を左に持っていけばいいことがわかります。
ということで重み($w$)を徐々に小さくしていってみましょう。
■重み($w$)を2にしてみる
$w=2のとき、90w_0 – 90 =90 × 2 – 90 =90$
傾きが減りましたね。
■重み($w$)を1にしてみる
$w=1のとき、90w_0-90=90 × 1-90=0$
傾きがゼロになりました!
■重み($w$)を-1にしてみる
$w=-1のとき、90w_0-90=90 × (-1)-90=-180$
あら、傾きがマイナスで出始めましたね。
ということで、(3.0)の重み($w_0$)が最小値になるのは$w_0=1$であることがわかりました。
もうお分かりかと思いますが、求めたかった式は、
いい感じの式 :$y_0 = x_0 + 4$ (1.2)
だったので、ばっちり$w_0=1$になりましたね。
で、どうやって重み($w$)を更新していきましょう?
今までは重み($w$)の値を変えながら、傾きがゼロになるところを探していましたが、そもそも重み($w$)は変数なので、何らかの計算の結果で重み($w$)を更新しなければいけませんね。
今、もっている情報としては、傾きを計算できる式(2.9)とテキトーに与える重み($w$)の初期値ですね。
先ほど重み($w$)の初期値3を入れたとき、傾きは180でした。この結果から重み($w$)軸を左に動かしていけば最小値に近づいていくことがわかります。
式にするとこんな感じです。
\begin{align}
w_n&=w_o – 傾き\\
&=w_o – (90w_o-90)
\end{align}
実際にやってみましょう。(今回求めたい重み($w$)の最小値は1です)
■重み($w$)を3にしてみる
$w_n=w_o – (90w_o-90)$
$-177 = 3 – ( 90 * 3 – 90 ) $
$15843 = -177 – ( 90 * -177 – 90 )$
$-1409937 = 15843 – ( 90 * 15843 – 90 )$
$125484483 = -1409937 – ( 90 * -1409937 – 90 )$
・・・
重み($w_n$)が1に近づく気配がまったくないですね・・・。
これは、最小値へ近づくための$w$が動く幅が大き過ぎることが原因なので、ここにある係数をかけて動く幅を小さくしましょう。
そのある係数のことを学習率と呼びます。
学習率は0.01と0.001とかで設定されることが多く、この学習率が小さければ小さいほど正確に学習できる可能性が高くなります。が、小さければ小さいほど、計算量は多くなるというデメリットがあります。
では、試しに先ほどの式に0.01をかけてみます。
$w_n=w_o – (90w_o-90)$
$1.2 = 3 – ( 90 * 3 – 90 ) (3.0)$
$1.02 = 1.2 – ( 90 * 1.2 – 90 ) $
$1.002 = 1.02 – ( 90 * 1.02 – 90 ) $
$1.0002 = 1.002 – ( 90 * 1.002 – 90 ) $
$1.00002 = 1.0002 – ( 90 * 1.0002 – 90 ) $
$1.000002 = 1.00002 – ( 90 * 1.00002 – 90 ) $
$1.0000002000000001 = 1.000002 – ( 90 * 1.000002 – 90 ) $
$1.00000002 = 1.0000002000000001 – ( 90 * 1.0000002000000001 – 90 ) $
$1.000000002 = 1.00000002 – ( 90 * 1.00000002 – 90 ) $
$1.0000000002 = 1.000000002 – ( 90 * 1.000000002 – 90 ) $
$1.00000000002 = 1.0000000002 – ( 90 * 1.0000000002 – 90 ) $
$1.000000000002 = 1.00000000002 – ( 90 * 1.00000000002 – 90 ) $
$1.0000000000002 = 1.000000000002 – ( 90 * 1.000000000002 – 90 ) $
$1.00000000000002 = 1.0000000000002 – ( 90 * 1.0000000000002 – 90 ) $
$1.000000000000002 = 1.00000000000002 – ( 90 * 1.00000000000002 – 90 ) $
$1.0000000000000002 = 1.000000000000002 – ( 90 * 1.000000000000002 – 90 ) $
$1.0 = 1.0000000000000002 – ( 90 * 1.0000000000000002 – 90 ) $
ぬぉ!重み($w_n$)が1になりました!!
これでいい感じの重み($w$)を見つけることができましたね。
今までやってきたことは言いかえると重み($w_i$)を更新する式の証明です。
重み($w_i$)を更新する式
\begin{align}
w_i&=w_i-η\frac{∂E}{∂w_i}\\
&=w_i−η(Σ((w_ix_i+b)−t_i)∗x_i)
\end{align}
式だけ見ると「何これ?」ってなりますが、かみ砕いていくとちゃんと理解できるもんですね。
念のため、重みを更新する式でやってみよう
$w_n=(w_o−η(((w_ox+b)−t)∗x))+(w_o−η(((w_ox+b)−t)∗x))$
$ =(w_0-0.01*(((w_0*3+4)−7)∗3)+(((w_0*9+4)−13)*9))$
$ =(w_0-0.01*((((w_0*3+4)−7)∗3)+(((w_0*9+4)−13)*9)))$
$ =(3-0.01*((((3*3+4)−7)∗3)+(((3*9+4)−13)*9)))$
$ =1.2$
さきほど手計算した(3.0)と一致するので、このまま計算を繰り返すと同じ結果が得られます。
いい感じのバイアス($b$)を見つけにいこう
最終的に求めたい式は、$y = x + 4$でした。つまり、バイアスが$4$に近づいてほしいわけです。
重みを見つけたときと同様、重みの定数を1として(2.3)の誤差を求める式に入れていきます。
$0 = b^2+12w_0b-20b+45w_0^2-138w_0+109$
$0 = b^2+12*1b-20b+45*1^2-138*1+109$
$0 = b^2 – 8b + 16$
グラフはこんな感じです。
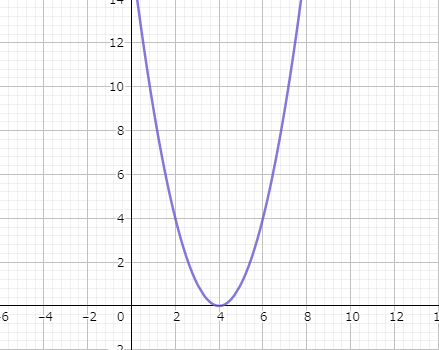
グラフから最小値になるバイアスは$4$であることがわかりますね。実際はこんな単純では・・・もういいっすね 笑
次は微分して傾きを求めるんでしたね。
$b^2 – 8b + 16$
$=2b – 8$
次にバイアスを$-8$と仮定して、●●の式で求めていきましょう。
$b_n=b_o – (2b-8)$
$-7.76 = -8 – ( 2 * (-8) – 8 ) (3.1)$
$-7.5248 = -7.76 – ( 2 * -7.76 – 8 ) $
$-7.294304 = -7.5248 – ( 2 * -7.5248 – 8 ) $
・
・
・
$3.996134912130708 = 3.9960560327864365 – ( 2 * 3.9960560327864365 – 8 ) $
$3.996212213888094 = 3.996134912130708 – ( 2 * 3.996134912130708 – 8 ) $
$3.9962879696103317 = 3.996212213888094 – ( 2 * 3.996212213888094 – 8 ) $
限りなく$4$に近づきましたね。あまりにも長くなってので中略しましたが、計算を400回繰り返しました。
バイアスの更新式でみてみよう
バイアスの更新式は以下の通りでした。
バイアスを更新する式
\begin{align}
b&=b-η\frac{∂E}{∂b}\\
&=b−η(Σ(w_ix_i+b)−t_i)
\end{align}
これに当てはめてみます。
$b_n=b_o-0.01*(((3*1+b_o)-7)+((9*1+b_o)-13)))$
$b_n=-8-0.01*(((3*1+(-8))-7)+((9*1+(-8))-13)))$
$b_n=-7.76$
さきほど手計算した(3.1)と一致するので、このまま計算を繰り返すと同じ結果が得られます。
まとめ
いかがでしたでしょうか。
公式自体は小難しいですが、やっていることはとてもシンプルであることが理解いただけたのではないでしょうか。
とは言うものの、まだフワフワしている感覚もあるかもしれませんが、一度、自分で問題設定をしてみて解いてみるのも一つの方法かと思います。
その時にようやく「なるほどね」となると思います。
ここまで読んでいただきありがとうございました。



コメント