3つ以上を分類(多値分類)する際、ニューラルネットワークの最終層で活性化関数としてソフトマックス関数が用いられる。(ちなみに2つを分類するにはシグモイド関数を利用。この章では取り扱わない。)
計算グラフ
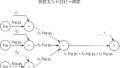
早速ですが、ソフトマックス関数の計算グラフについて確認してみます。
.png)
なぜ計算グラフで理解するのか?
計算グラフで理解するメリットは2つあります。
・難しい計算式を分解し部品化することで「処理の流れ」を簡単に理解することができる
・図で理解するので、忘れにくい。
計算グラフの解説
これを踏まえて先ほどの計算グラフを見てみましょう。
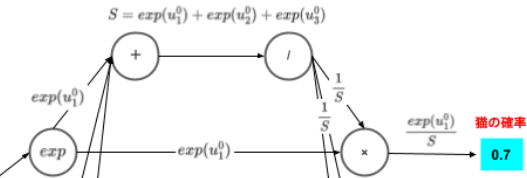
上流からインプットとして$u$が流れてきて、$exp$に到達したあと2系統に分かれています。1つは$×$へ伝達するもの、もう一つは$+$に伝達するもの。
$+$の方向では、他の$exp$からも値が伝達されており、伝達された3つの値を$+$で総和をとっています。その後は$/$で逆数をとり、元の経路$×$へ戻していることがわかります。
あとはそれぞれの経路で$×$で処理をし、終了です。
このように計算の過程を「流れ」として捉えることで、小難しい式をシンプルに理解することができます。
ソフトマックス関数は比較的単純な式のため、計算グラフの有難みを感じにくいかもしれませんが、交差エントロピー誤差や誤差逆伝播のような複雑な処理においてその効果を最大限に発揮してきます。
これを機に計算グラフをしっかり理解することをお勧めします。
ここからは具体的な処理を交えながらソフトマックス関数の理解を進めていきます。
簡単なイメージ
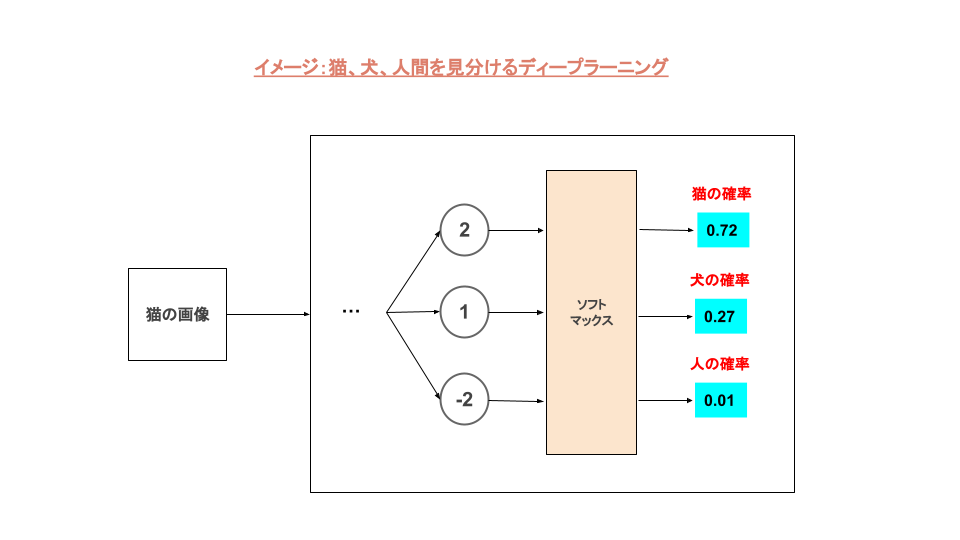
入力した画像をすべてのニューロンに伝え、それぞれの過程で計算され出力された結果をソフトマックス関数で確率に変換します。
上の図ではソフトマックス関数によって、猫:72%、犬:27%、人:1%として確率変換されました。
次に実際にどのように確率変換されているのかをみていきます。
確率変換の手順は3つ
①ニューロンの出力結果を指数関数で計算する
入力画像が伝達される過程で計算された結果(今回の場合[2,1,-2])を指数関数\(exp\)で計算します。
import numpy as np
a = np.array([2,1,-2]) # 伝達される過程で計算された結果
print(a)
## [ 2 1 -2]
exp_a = np.exp(a) # 指数関数 e で計算
print(np.round(exp_a,1))
## [7.4 2.7 0.1]②指数関数\(exp\)結果の総和をとる
つづいて、指数関数\(exp\)で計算した結果の総和をとります。
np.sum(exp_a)
## 10.242673210626307単純に足しているだけですね。
③最後に「①÷②」する
最後は「①÷②」で計算します。
softmax_a = exp_a[0] / np.sum(exp_a)
softmax_b = exp_a[1] / np.sum(exp_a)
softmax_c = exp_a[2] / np.sum(exp_a)
print(softmax_a) ## 0.7213991842739688
print(softmax_b) ## 0.26538792877224193
print(softmax_c) ## 0.013212886953789417それぞれの出力結果から、猫:72%、犬:27%、人:1%と冒頭のイメージ図通りの確率になりました。
単純に総和せず、\(exp\)を使う理由
それぞれの値を総和で割るなら\(exp\)を使わずに単純な総和で割っても一緒でしょ?という疑問を持つ方もいると思います。
結論から先にいうと「マイナスの値をうまく考慮するため」です。
実際に検証していきます。
単純に足し算した場合
import numpy as np
a = np.array([2,1,-2])
print(a)
## [ 2 1 -2]
add_a = a[0] / np.sum(a)
add_b = a[1] / np.sum(a)
add_c = a[2] / np.sum(a)
print(add_a) ## 2.0
print(add_b) ## 1.0
print(add_c) ## -2.0猫:200%、犬:100%、人:-200%という結果になりました。
計算する値にマイナスがあるため、単純に足すだけではダメだということがわかりました。
絶対値をとった場合
マイナスをプラスとして処理する方法として絶対値をとる方法があります。
実際に検証してみましょう。
import numpy as np
a = np.array([2,1,-2])
print(a)
## [ 2 1 -2]
## 絶対値へ変換
abs = np.abs(a)
print(abs)
## [2 1 2]
abs_a = abs[0] / np.sum(abs)
abs_b = abs[1] / np.sum(abs)
abs_c = abs[2] / np.sum(abs)
print(abs_a) ## 0.4
print(abs_b) ## 0.2
print(abs_c) ## 0.4単純な足し算とは違い、すべの確率を足すと100%になるので確率計算としてはうまくいきました。
結果をみてみると、猫:40%、犬:20%、人:40%となっています。この画像は猫でしたが、人の確率がぐっと上がっていることがわかります。
言い換えると、猫の画像を入れて猫か人かわからないような結果になっているとも言えます。これでは使いものにならないですね。
\(exp\)を使う理由
入力画像に猫を入れて、ニューラルネットワーク内で計算された結果 [ 2 , 1 , -2 ] が出力されています。
左から [ 猫 , 犬 , 人 ] であったので、それぞれの数字の意味として数字の大小関係が分類に影響していることがわかります。
つまり、この大小関係を保ちつつ、確率化するためには\(exp\)が適しているということです。
公式
この流れは次の式で定義されます。
\( y_k = \dfrac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i)}\)
公式にすると一気に難しく見えますが、上で説明したように非常にシンプルです。
ミニバッチ版
次は実践でよく利用されるミニバッチ版でのソフトマックス関数をみていきます。
今までの説明はソフトマック関数が本来持つ本質を理解してもらうための説明でしたが、実際の実装においてはもう少し考慮が必要な要素がでてきます。
その点を踏まえて、より実践的な解説をしていきます。
配列の形状を意識する
ミニバッチ版でもやっていることの本質は変わりませんが、配列の形状を意識しないと実装できない(できても意図とは違う結果になる)ケースがあります。
まずは結果から
まずは最終的に実装される内容を提示しておきます。この時点でコード内容を理解する必要はありませんが、本質的には今まで説明してきたことと一緒なんだな、ということは覚えておいてください。
## ソフトマックス関数
def softmax(y):
_o = y - np.max(y,axis=1,keepdims=True)
return np.exp(_o) / np.sum(np.exp(_o),axis=1,keepdims=1)説明の前提
今までの説明では分類したい画像を1つ入力し、[ 猫 , 犬 , 人 ]のいづれなのかを予測するものでした。
今回、分類する種類はそのままで、入力する画像を2つにして説明をします。
入力データの形状
はじめに入力データを準備します。
1つ目のデータは先ほど同様「猫」で、2つ目のデータは「人」にします。
import numpy as np
y = np.array([[2,1,-2],[3,5,7]]) ## 猫と人の画像
print(y)
## [[ 2 1 -2]
## [ 3 5 7]]当たり前ですが、2つの画像をインプットしているので、2行のデータになっています。
念のため、.shapeで形状を確認しておきます。
print(y.shape) ##(2, 3)想定通り、入力データの形状は2行3列になっています。
各行単位でソフトマックス関数を施す
つづいて、各行単位でソフトマックス関数を施します。
各行とは「猫」と「人」の各画像のことを指しますので、各行単位でソフトマックス関数処理し、確率を求めます。
①各行内の最大値取得する
まず、各行から配列の形状を保持したまま、最大値を取得します。(最大値を取得する意味はこのあとすぐ説明します)
np.max(y,axis=1,keepdims=True)
## [[2]
## [7]]このとき単純にnp.maxしてはいけません。
なぜなら、配列内のすべての要素から最大となる1つの値を取得しまうためです。
そのためにaxisで取得する方向を指定します。
各行(横方向)から最大値を取得する場合、axis=1と指定します。
もう一つ大切なのが、配列の形状を保つためにkeepdims=Trueを指定しておく必要があります。
形状を保たないと、このあとの計算で「配列の形状が違うから計算できないよ」とエラーになってしまいます。
②各行各値から最大値を引く
つぎに、各行の各値からさきほど取得した最大値を引きます。
理由は、計算過程でオーバーフロー回避するため、です。
ソフトマックス関数では$exp$で計算をするため、指数となる数が大きくなると結果も指数的に大きくなるため、計算結果がオーバーフローを起こしてしまう可能性があります。
オーバーフローを回避するため、各行の最大値を各値から引きます。
同じ値を各値から引いているので、確率計算には影響を与えないのがポイントです。
_o = y - np.max(y,axis=1,keepdims=True) ##[[ 0 -1 -4]##[-4 -2 0]]
③総和を求める
確率を求めるためには各行の値を各行の総和で割れば求められますね。
先程と同様、各行の総和を求める場合、足す方向を指定する必要があります。
そのためにaxisで足す方向を指定します。
各行(横方向)の総和を求める場合、axis=1と指定します。
## 各行の総和を求める
np.sum(np.exp(y),axis=1,keepdims=True)もう一つ、次元をキープするためにkeepdims=Trueを指定します。
最後に「②÷③」する
最後は②÷③をして終了です。
def softmax(y):
_o = y - np.max(y,axis=1,keepdims=True)
return np.exp(_o) / np.sum(np.exp(_o),axis=1,keepdims=True)o = softmax(y) print(o) ##[[0.72139918 0.26538793 0.01321289]##[0.01587624 0.11731043 0.86681333]]
【再掲】計算グラフ
最後にソフトマックス関数の計算グラフを再掲します。
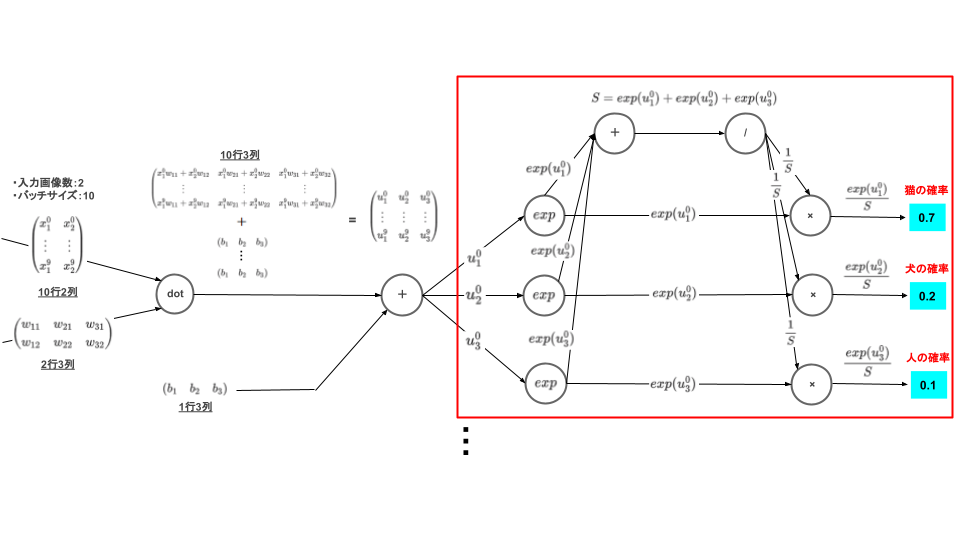
冒頭にも説明しましたが、計算グラフで表現すると値と処理の流れが可視化されるため、非常に理解が進みます。ソフトマックス関数の順伝播のようなシンプルな処理ではそれほど計算グラフの効果は感じられませんが、複雑な処理の場合、計算グラフはその威力を発揮します。特に誤差逆伝播法では最大限にその効果が感じられることでしょう。
まだ計算グラフに見慣れていない方は、是非マスターすることをおすすめします。
次回はソフトマックス関数と同時に語られる交差エントロピー誤差について解説を予定しています。
コメント